Lesson 3 Euclid Geometry
DEAR STUDENTS
WELCOME TO THE CLASS!!
FEW REMINDERS:
The text in Red, is to be written in your register
·
Yesterdays learning outcomes
1. Recall Euclid's axioms and postulate
1. Recall Euclid's axioms and postulate
1. Take your Mathematics Register
2. Our handwriting reflects a lot about us. It will be awesome if you use good presentation and cursive hand writing
3. Make a column on the right hand side, if you need to do any rough work
4. Leave two lines where you finished yesterday’s work and draw a horizontal line
5. Write today's date on the line after that.
6. Pending Queries from yesterday (if any).......
7. Please write the learning outcomes as mentioned below
Today's learning outcomes are
I will be able to:
1. recall, THE POSTULATES
1. recall, THE POSTULATES
2.recall , PLAYFAIR'S AXIOM
Postulate – II
Any straight line can be extended indefinitely on both sides. Unlike a line segment, a line is not bounded by any endpoint and so can be extended indefinitely in either direction. A line is uniquely defined as passing through two points which are used to name it.
Postulate – III
A circle can be drawn with any centre and any radius. For any line segment, a circle can be drawn with its centre at one endpoint and the radius of the circle as the length of the line segment. Consider a line segment bounded by two points. If one of these points is taken as the centre of a circle and the radius of the circle is taken as equal to the length of the segment, a circle can be drawn with its diameter twice than the length of the line segment.
Postulate – IV
All right angles are congruent or equal to one another. A right angle is an angle measuring 90 degrees. So, irrespective of the length of a right angle or its orientation all right angles are identical in form and coincide exactly when placed one on top of the other.

A right angle
click on the link 👇 to know 5th postulate and Playfair's Axiom
 ‘Parallel lines’ are a set of 2 or more lines that never cross or intersect each other at any point in space if they are extended indefinitely. As you can see in the above image, line 1 and line 2 are parallel if and only if the sum of angles ‘a’ and ‘b’ they make with the transversal is 180 degrees.
‘Parallel lines’ are a set of 2 or more lines that never cross or intersect each other at any point in space if they are extended indefinitely. As you can see in the above image, line 1 and line 2 are parallel if and only if the sum of angles ‘a’ and ‘b’ they make with the transversal is 180 degrees.
Postulate – V
Two lines are parallel to each other if they intersect the third line and the interior angle between them is 180 degrees.
PLAYFAIR'S AXIOM
- This is equivalent version of Euclid fifth law which states lines will not intersect when the angle is equal two right angle
lets TEST ourself by completing the given crossword
Crossword for Euclid Geometry
1. He was the student of Thales.
8. The terms specifically used for assumption in Geometry.
9. A _______ is a theorem that is usually considered an "easy consequence" of another theorem.
Down
2. Square and circular ____ were used for household rituals.
3. The instrument consists of nine interwoven isosceles triangles
4. Euclid was a teacher of mathematics in Alexandria in _______
5. Thales belongs to ______
6. They are the statements which are proved
7. The term used for the assumptions which are used throughout mathematics
Don't worry if you couldn't attempt all. Answers are given .
Exercise 5.2 (To be done in register) HW
ALSO THE SOLVED EXAMPLES
1. How would you rewrite Euclid’s fifth postulate so that it would be easier to understand?
Solution:
Euclid’s fifth postulate: If a straight line falling on two straight lines makes the interior angles on the same side of it taken together less than two right angles, then the two straight lines, if produced indefinitely, meet on that side on which the sum of angles is less than two right angles.
i.e., the Euclid’s fifth postulate is about parallel lines.
Parallel lines are the lines which do not intersect each other ever and are always at a constant perpendicular distance apart from each other. Parallel lines can be two or more lines.
A: If X does not lie on the line A then we can draw a line through X which will be parallel to that of the line A.
B: There can be only one line that can be drawn through the point X which is parallel to the line A.
Q2. Does Euclid’s fifth postulate imply the existence of parallel lines? Explain.
Solution:
Yes, Euclid’s fifth postulate does imply the existence of the parallel lines.
If the sum of the interior angles are equal to the sum of the right angles, then the two lines will not meet each other at any given point, hence making them parallel to each other.
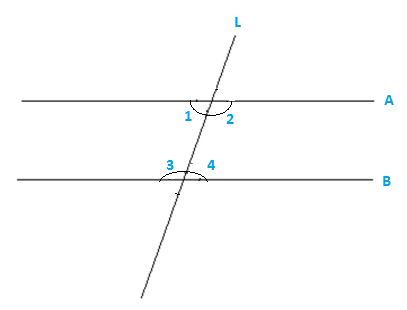
∠1+∠3=180o
Or ∠3+∠4=180o
HOME WORK Also Learn all the axioms and postulates
Cross word
Answers
1. Pythagoras
2. altars
3. sriyantra
4. Egypt
5. Greece
6. Theorem
7. axiom
8. postulate
9. Corollary
2. altars
3. sriyantra
4. Egypt
5. Greece
6. Theorem
7. axiom
8. postulate
9. Corollary
Thats all for the day
Have a good day 😄




GOOD MORNING MAM
ReplyDeleteTHIS IS ARHAM KHAN
CLASS-9B
Good morning ma'am
ReplyDeleteSubhamay pandit
9B
Good Morning Ma'am
ReplyDeleteAaditya Sabharwal
9B
GOOD MORNING MA'AM
ReplyDeleteTHIS IS DINU V THOMAS
9-B
vansh gupta
ReplyDeleteShaurya Srivastava 9B
ReplyDeleteGood morning Ma'am
ReplyDeleteAchintya from 9 B