LESSON 2 NUMBER SYSTEM
Dear Students,
Welcome to the second class of this session !!
General Instructions:
1. All of you will maintain 2 registers for Maths ( Set A and Set B) plus 1 practical file(you will be explained about the practical work later).
2. Make the index including S.No. ,Date,Topic,Sign.
Guidelines for the Blog
· The text in Red, is to be written in your register
· The text in blue is to be viewed by clicking on it
· The text in green is to be practiced for home work
· Feel free to clarify your doubts by dropping a comment before going ahead in the lesson.
Dear Students,
Welcome to the second class of this session !!
General Instructions:
1. All of you will maintain 2 registers for Maths ( Set A and Set B) plus 1 practical file(you will be explained about the practical work later).
2. Make the index including S.No. ,Date,Topic,Sign.
Guidelines for the Blog
· The text in Red, is to be written in your register
· The text in blue is to be viewed by clicking on it
· The text in green is to be practiced for home work
· Feel free to clarify your doubts by dropping a comment before going ahead in the lesson.
- Take your SET-A Mathematics Register
- Our handwriting reflects a lot about us. It will be awesome if you use good presentation and cursive hand writing
- Make a column on the right hand side, if you need to do any rough work
Write today's date on the line after that. We need to save paper. Write the SDG – 12 : Responsible Consumption and Production. Let us be responsible global citizens. One good thing that Coronovirus is teaching us! That is be responsible global citizens.Please write the learning outcomes as mentioned below :
I will be able to:
I will be able to:
·What are Irrational numbers
Locating Irrational numbers on a number line.
Lets recall yesterdays conceptsNATURAL ,WHOLE .INTEGERS AND RATIONAL NUMBERSWHAT ARE IRRATIONAL NUMBERS ?

An Irrational Number is a real number that cannot be written as a simple fraction.Irrational means not Rational

Let's look at what makes a number rational or irrational ...click the link given below
link Rational Numbers
A Rational Number can be written as a Ratio of two integers (ie a simple fraction).
Example: 1.5 is rational, because it can be written as the ratio 3/2 Example: 7 is rational, because it can be written as the ratio 7/1 Example 0.333... (3 repeating) is also rational, because it can be written as the ratio 1/3
Irrational Numbers
But some numbers cannot be written as a ratio of two integers ...
...they are called Irrational Numbers.
Example: π (Pi) is a famous irrational number.

π = 3.1415926535897932384626433832795... (and more)We cannot write down a simple fraction that equals Pi.
The popular approximation of 22/7 = 3.1428571428571... is close but not accurate.
Another clue is that the decimal goes on forever without repeating.
Cannot Be Written as a Fraction
It is irrational because it cannot be written as a ratio (or fraction),not because it is crazy!So we can tell if it is Rational or Irrational by trying to write the number as a simple fraction.
Example: 9.5 can be written as a simple fraction like this:
9.5 = 192So it is a rational number (and so is not irrational)
Here are some more examples:
Square Root of 2
Let's look at the square root of 2 more closely.
The answer is the square root of 2, which is 1.4142135623730950...(etc)But it is not a number like 3, or five-thirds, or anything like that ...
... in fact we cannot write the square root of 2 using a ratio of two numbers
... I explain why on the Is It Irrational? page,
... and so we know it is an irrational number
link Rational Numbers
A Rational Number can be written as a Ratio of two integers (ie a simple fraction).
Example: 1.5 is rational, because it can be written as the ratio 3/2 Example: 7 is rational, because it can be written as the ratio 7/1 Example 0.333... (3 repeating) is also rational, because it can be written as the ratio 1/3
Irrational Numbers
But some numbers cannot be written as a ratio of two integers ...
...they are called Irrational Numbers.
Example: π (Pi) is a famous irrational number.

π = 3.1415926535897932384626433832795... (and more)We cannot write down a simple fraction that equals Pi.
The popular approximation of 22/7 = 3.1428571428571... is close but not accurate.
Another clue is that the decimal goes on forever without repeating.
Cannot Be Written as a Fraction
It is irrational because it cannot be written as a ratio (or fraction),not because it is crazy!So we can tell if it is Rational or Irrational by trying to write the number as a simple fraction.
Example: 9.5 can be written as a simple fraction like this:
9.5 = 192So it is a rational number (and so is not irrational)
Here are some more examples:
| Number | As a Fraction | Rational or Irrational? | ||
|---|---|---|---|---|
| 1.75 | 74 | Rational | ||
| .001 | 11000 | Rational | ||
| √2 (square root of 2) | ? | Irrational ! |
Let's look at the square root of 2 more closely.
 | When we draw a square of size "1", what is the distance across the diagonal? |
... in fact we cannot write the square root of 2 using a ratio of two numbers
... I explain why on the Is It Irrational? page,
... and so we know it is an irrational number
FAMOUS IRRATIONAL NUMBER
 | Pi is a famous irrational number. People have calculated Pi to over a quadrillion decimal places and still there is no pattern. The first few digits look like this: 3.1415926535897932384626433832795 (and more ...) | |||||
 | The number e (Euler's Number) is another famous irrational number. People have also calculated e to lots of decimal places without any pattern showing. The first few digits look like this: 2.7182818284590452353602874713527 (and more ...) | |||||
 | The Golden Ratio is an irrational number. The first few digits look like this: 1.61803398874989484820... (and more ...) | |||||
 | Many square roots, cube roots, etc are also irrational numbers. Examples:
|
But √4 = 2 (rational), and √9 = 3 (rational) ...... so not all roots are irrational.. Let's answer:- ( IN COMMENTS COLUMN ) IN BLOQ2.
Let's answer:- ( IN COMMENTS COLUMN ) IN BLOQ2.
 Let's answer:- ( IN COMMENTS COLUMN ) IN BLOQ2.
Let's answer:- ( IN COMMENTS COLUMN ) IN BLOQ2.
Exercise 1.2
Q1. State whether the following statements are true or false. Justify your answers.(i)Every irrational number is a real number.

Q2. Are the square roots of all positive integers irrational? If not, give an example of the square root of a number that is a rational number.

Q3. Show how square root of 5 can be represented on the number line.

click on the link to represent √2 on a number line https://youtu.be/2bMKu1CXyB0
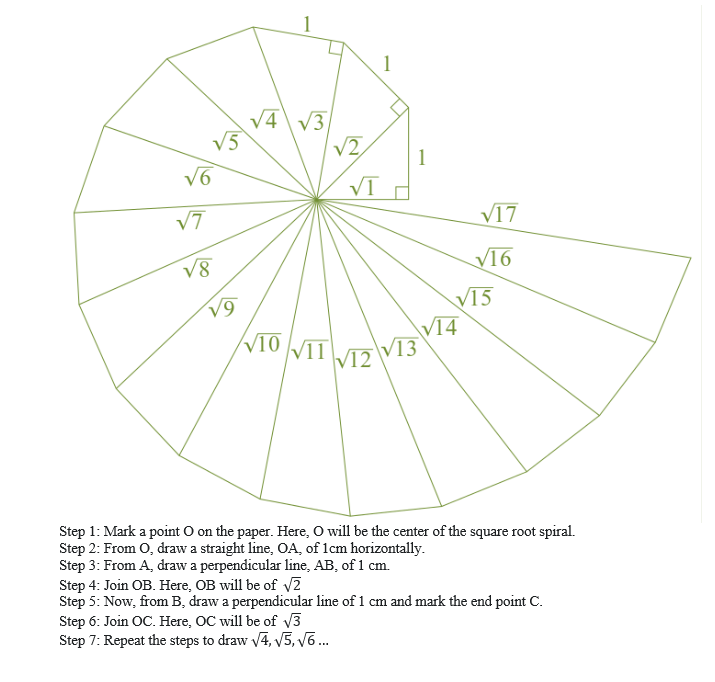
NOTE: Q4 TO BE DONE IN MATHS PRACTICAL FILE (ACTIVITY NO. 1 )Q4. Classroom activity (Constructing the ‘square root spiral’) : Take a large sheet of paper and construct the ‘square root spiral’ in the following fashion. Start with a point O and draw a line segment OP1 of unit length. Draw a line segment P1P2 perpendicular to OP1 of unit length (see Fig. 1.9). Now draw a line segment P2P3 perpendicular to OP2. Then draw a line segment P3P4 perpendicular to OP3. Continuing in Fig. 1.9 :
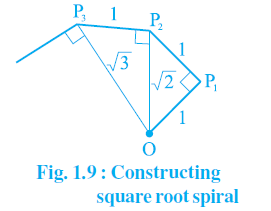
Constructing this manner, you can get the line segment Pn–1Pn by square root spiral drawing a line segment of unit length perpendicular to OPn–1. In this manner, you will have created the points P2, P3,…., Pn,… ., and joined them to create a beautiful spiral depicting 2, 3, 4, …Solution:
CLICK ON THE LINK TO KNOW ABOUT 17 SUSTAINABLE DEVELOPMENT GOALSThats all for today.Take care .


vansh gupta
ReplyDeleteMy name is Subhamay Pandit 9B
ReplyDeleteGood morning ma'am
Good morning ma'am
ReplyDeleteMisbah-ul-haq
9B
Good morning ma'am
ReplyDeleteAnurag S Peter 9B
Ashish malhotra
ReplyDelete9b
Good morning ma'am I am Maximus Haokip of class 9-B
ReplyDeleteGood Morning Maam
ReplyDeleteAaditya Sabharwal
9B
Good morning mam
ReplyDeleteRishabh Gupta 9B
Presley Joseph 9b
ReplyDeleteGood morning ma'am I'm Shan Babu 9 B
ReplyDeleteGood Morning Ma'am
ReplyDeleteMY NAME IS ANUGRAH JOEL
Class 9B
Good morning Ma'am
ReplyDeleteMy name is Abhijai Chugh
Good morning ma'am
ReplyDeleteAryan Nirmal from 9-B
GOOD MORNING MA'AM
ReplyDeleteI AM SAKSHAM ARORA
GOOD MORNING MAM
ReplyDeleteTHIS S ARHAM KHAN
CALSS-9B
Good morning ma'am
ReplyDeleteThis is Edwin Tom Benoy 9B
My name is Lakshay Bansal 9b
ReplyDeleteApril 01 2020
ReplyDeleteGood morning ma'am
Rishi Bhardwaj
9B
Good Morning Ma'am,
ReplyDeletePulak Gola-9-B
Good Morning Mam
ReplyDeleteYash Verma
IX B
Good Morning Ma'am
ReplyDeleteThis is Daniel Vincent
Class:9B
Good morning ma'am.
ReplyDeleteThis is Gurveer Singh(9B).
Good morning ma'am
ReplyDeleteShaurya Srivastava 9B
Good Morning ma'am
ReplyDeleteRachit Kerketta (9-B)
Good morning ma'am
ReplyDeleteAron Thomas
9-B
Good Morning Madame
ReplyDeleteThis is Jeril James 9B
GOOD MORNING MA'AM
ReplyDeleteMADHAV SHARMA
9B
Good morning ma'am I am Ryan Daniel of class 9-B
ReplyDeleteDaniel Benjamin
ReplyDelete9B
Good morning ma'am.
ReplyDeleteThis is Ipsit A Kakoty of 9-B.
Good afternoon ma'am.
ReplyDeleteThis is Ipsit A Kakoty of 9-B.
GOOD MORNING MAAM
ReplyDeleteAASHMAN TIWARI HERE
9B
Good morning ma'am
ReplyDeleteAnurag S Peter 9B
This comment has been removed by the author.
ReplyDeleteGood Morning Ma'am
ReplyDeleteMy name is Anugrah Joel (9B)