POLYNOMIALS ( LECTURE 7)

LESSON 7 POLYNOMIALS

GOOD MORNING STUDENTS



yesterdays ' learning outcomes were:


I will be able to factorize polynomials by using

Todays learning outcomes  I will be able to 
 find the value of "k" 
factorise  a quadratic polynomial (splitting the middle term)
factorise a cubic polynomial

AQAD
1) Find the remainder  when x4+x3-2x2+x+1 is divided by x-1
 a)1
b)5
c)2
d)3



FEW INSTRUCTIONS
 The content in BLUE have to be written in the register as cw.

NOW LETS SOLVE Question 3.(EX 2.4)
Find the value of k, if x- 1 is a factor of p(x) in each of the following cases:

(ii)$p\left(x\right)=2x^2+kx+\sqrt{2}$
$p(x)=k{x}^2-\sqrt{2}$
(iv)$p\left(x\right)=k{x}^2-3x+k$
Solution LETS  SOLVE (ii) 

(ii) If x- 1 is a factor of polynomial 

$p\left(x\right)=2x^2+kx+\sqrt{2}$, then (USING FACTOR THEOREM) 
$p\left(1\right)=0$
$2(1{)}^2+k(1)+\sqrt{2}=0$
$k=-2-\sqrt{2}=-(2+\sqrt{2})$
So, value of k is $-(2+\sqrt{2})$.


(iv) If x- 1 is a factor of polynomial 
$p\left(x\right)=k{x}^2-3x+k$, then
$p\left(1\right)=0$
$k(1{)}^2+3(1)+k=0$
$k-3+k=0$
$k=\frac{3}{2}$
So, value of k is $\frac{3}{2}$

 Lets recall factorising quadratic polynomial by splitting the middle term


 .CLICK THE GIVEN LINK FOR  FACTORISATION OF QUADRATIC POLYNOMIAL

factorise quadratic polynomial


 LETS TAKE AN  EXAMPLE  ( TO  FACTORISE)  
Example 1 : 4x2 + 12x + 5
Solution: We have to find two numbers, whose
sum is 12 (middle term) and when
multiplied (first and last term) i.e. 4 X 5 we get 20

So these two numbers are -
10 + 2 = 12
10 X 2 = 20

Now we put both 10 and 2 numbers in the middle term of 12x and we get

∴ 4x2 + 12x + 5
 = 4x2 + 10x + 2x + 5
or 2x(2x + 5) + 1(2x + 5)
or (2x + 5)(2x + 1)

Try       4x2 + 8x - 5  (CW)         Ans ((2x + 5)(2x - 1)


solve Q3 of ex 2.4
Question 4
Factorise:
(i) $12x^2+7x+1$

lets solve 
Solution
Here we would be using splitting the middle term to factorise the polynomial
To factorise $a{x}^2+bx+c$, we should write b as the sum of two numbers whose product is ac
(i) $12x^2+7x+1$
Here a=12, c=1 and b=7 So $b=7=3+4$ ,$ac=12\times 1=12=3\times 4$
$12x^2+7x+1$
$=12x^2+4x+3x+1$
$=4x(3x+1)+1(3x+1)$
$=(3x+1)(4x+1)$


(iv) $3x^2-x-4$
Here a=3, c=-4 and b=-1 So, $b=-1=-4+3$, $ac=3\times (-4)=-12=(-4)\times 3$
$=3x^2-4x+3x-4$
$=x(3x-4)+1(3x-4)$
$=(3x-4)(x+1)$
  Lets see the video how to factorise cubic polynomial. click 👇 



$\mathrm{factorising\; cubic\; polynomialQ5}$
Factorise:

(i) $x^3-2x^2-x+2$

Solution
These are cubic polynomials and can be factorized using combination of long division method , remainder theorem and split middle term method
(i) Let $p\left(x\right)=x^3-2x^2-x+2$

STEP 1       Factors of 2 are ±1 and ± 2

STEP 2       By trial method, we find that

$p(-1)=(-1{)}^3-2(-1{)}^2-(-1)+2=0$(
$P(-1)=(-1{)}^3-2(-1{)}^2-(-1)+2=0$
STEP 3:-   So,(x+1) is factor of p(x)

. STEP 4  :-Now using the Long division method , we can find the quotient as

STEP 5 :-  Now, $Dividend=Divisor\times Quotient+Remainder$
$x^3-2x^2-x+2=(x+1)(x^2-3x+2)$

Factorizing the second part by split middle term method
$=(x+1)(x^2-x-2x+2)$
$=(x+1)\left[x\right(x-1)-2(x-1\left)\right]$
$=(x+1)(x-1)(x+2)$

Q5 (ii) $x^3-3x^2-9x-5$
LETS  SEE( ii) PART TOO 



(ii) Let 
$p\left(x\right)=x^3-3x^2-9x-5$
Factors of 5 are ±1 and ±5
By trial method, we find that
$p\left(5\right)=5^3-3\times 5^2-9\times 5-5=0$
So,(x-5) is factor of p(x)
Now using the Long division method , we can find the quotient as

Now, $Dividend=Divisor\times Quotient+Remainder$
$x^3-3x^2-9x-5=(x-5)(x^2+2x+1)$
Factorizing the second part by split middle term method
$=(x-5)(x^2+x+x+1)$
$=(x-5)x(x+1)+1(x+1)$
$=(x-5)(x+1)(x+1)$

HOME WORK  remaining parts 
(iii) $x^3+13x^2+32x+20$


(iv) $2y^3+y^2-2y-1$

I would encourage the students to try  and then check your answer.


(iii) Let $p\left(x\right)=x^3+13x^2+32x+20$
Factors of 20 are ±1, ±2, ±4, ±5, ±10 and ±20
By trial method, we find that
$p(-1)=(-1{)}^3+13(-1{)}^2+32(-1)+20=0$
So,(x+1) is factor ofp(x)
Now using the Long division method , we can find the quotient as

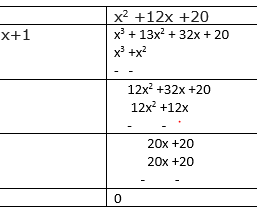
Now, Dividend = Divisor \times Quotient+ Remainder
$x^3+13x^2+32x+20=(x+1)(x^2+12x+20)$
Factorizing the second part by split middle term method
$=(x+1)(x^2+2x+10x+20)$
$=(x-5)\left[x\right(x+2)+10(x+2\left)\right]$
$=(x-5)(x+2)(x+10)$

(iv) Let $p\left(y\right)=2y^3+y^2-2y-1$
Factors of ab = 2 \times (-1) = -2 are ±1 and ±2
By trial method, we find that
$p\left(1\right)=2(1{)}^3+(1{)}^2-2\left(1\right)-1=0$
So,(y-1) is factor of p(y)
Now using the Long division method , we can find the quotient as

Now, $Dividend=Divisor\times Quotient+Remainder$
$\mathrm{Dividend=Divisor\times Quotient+Remainder2}{y}^3+y^2-2y-1=(y-1)(2y^2+3y+1)$
Factorizing the second part by split middle term method
$=(y-1)(2y^2+2y+y+1)$
$=(y-1)\left[2y\right(y+1)+1(y+1\left)\right]$
$=(y-1)(2y+1)(y+1)$

 HOMEWORK  
I would encourage the students to try  and then check your answer.

Q3,Q4 (remaining parts )
Factorize the  following

1. 3x3 –x2-3x+1
2. x3-23x2+142x-12

Answer
a) )(3x-1)(x-1)(x+1)
b)(x-1)(x-10)(x-12)

   AQAD     Solution ( c)


Q3 solution
(i) If x- 1 is a factor of polynomial $p\left(x\right)=x^2+x+k$, then
$p\left(1\right)=0$
$(1{)}^2+1+k=0$
$2+k=0$
$k=-2$

So, value of k is -2.
(iii) If x- 1 is a factor of polynomial $p\left(x\right)=k{x}^2-\sqrt{2}x+1$, then
$p\left(1\right)=0$
$k(1{)}^2-\sqrt{2}(1)+1=0$
$k=\sqrt{2}-1$

So, value of k is $\sqrt{2}-1$
$\mathrm{Q4\; (ii\; )2}{x}^2+7x+3$
Here a=2, c=3 and b=7 So $b=7=6+1$ ,$ac=2\times 3=6=6\times 1$
$=2x^2+6x+x+3$
$=2x(x+3)+1(x+3)$
$=(x+3)(2x+1)$

(iii) $6x^2+5x-6$
Here a=6, c=-6 and b=5 So, $b=5=9+(-4)$ ,$ac=6\times (-6)=-36=9\times (-4)$
$=6x^2+9x-4x-6$
$=3x(2x+3)-2(2x+3)=$